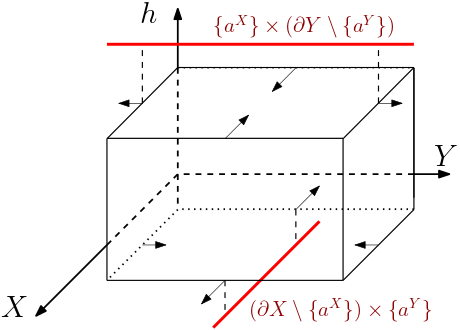Some figures from various research projects I worked on.
Quasi-isometry rigidity of quasi-isometry between horospherical products
Key elements of the proof of the splitting property of quasi-isometry in horospherical products.
A subdivision of a quasi-geodesic, leading to their coarse differentiation in a horospherical product.
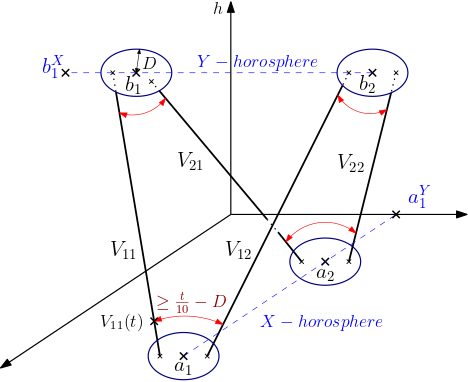
A specific configuration of four points linked by vertical geodesics, we call it vertical quadrilateral. It contains the metric rigidity behaviour of horospherical products.
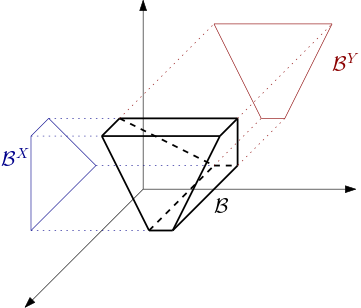
A box of the tiling of a horospherical product. This tiling is well suited for working along with the vertical flow of the spaces.
Geodesic and Visual boundary in horospherical products
The geometry of a horospherical product are quite rigid. It allows us to provide a description of its geodedesics and visual boundary.
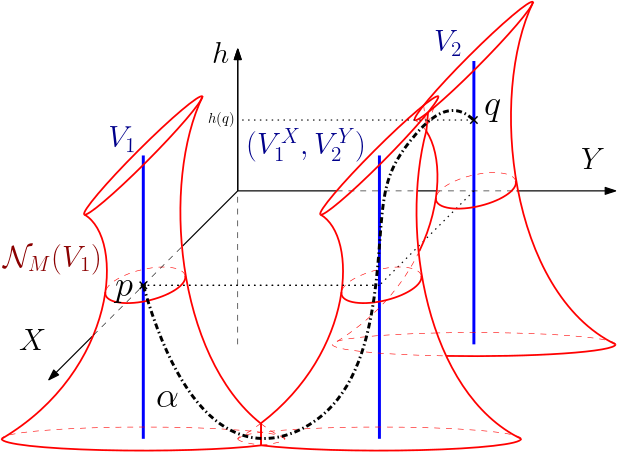
Three vertical geodesics (in blue), surrounded by their constant neighbourhood. Since the metric is distorded in the Sol geometry, by staying close to these vertical geodesics, we can travel along them by going sufficiently hight or down.
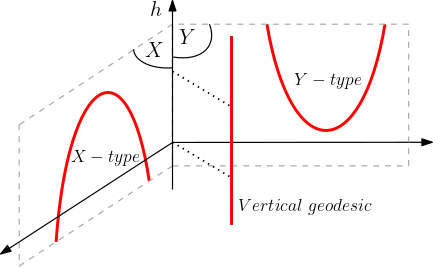
The only three possible shapes of bi-infinite geodesics in a horospherical product.
A way of understanding the description of the visual boundary of a horospherical product.
Separating profil and tree witdh
Master thesis under the supervision of Jeremie Brieussel.
Hurwitz Problem
Master internship at Pisa university, c, who made these three figures. They represent some combinatorial events for paths in a specific exagon tiling of the torus.
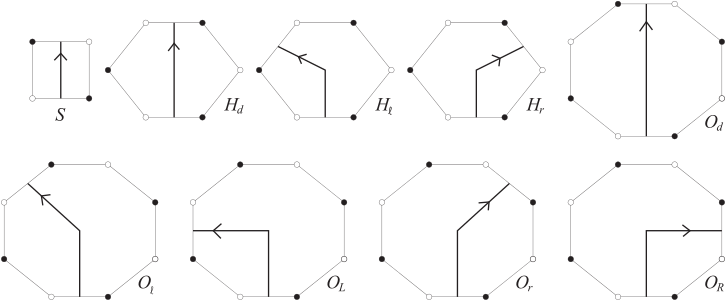
Possible crossings of a tile by a loop in a torus tiling.
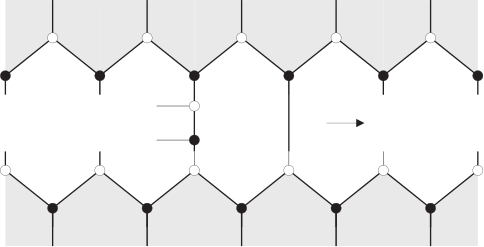
A way of optimizing the path in a (almost-)hexagonal tiling of a torus
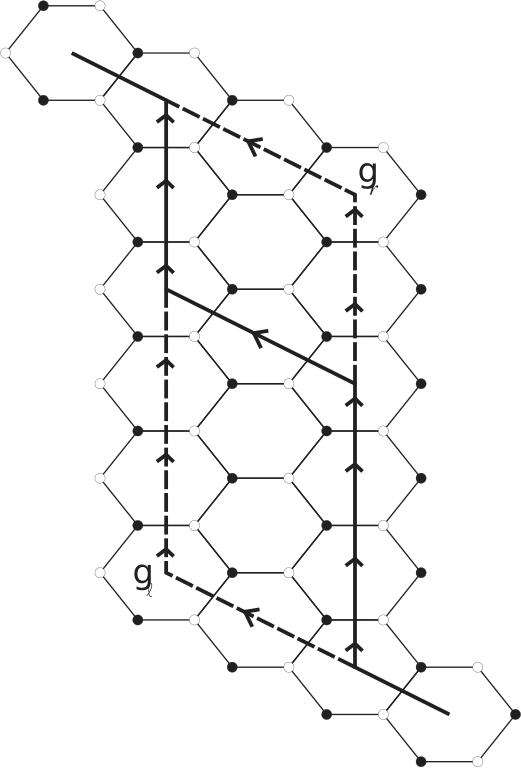
A specific configuration of a bicolor hexagonal tiling of the torus, which end up to close like a Zip.